| ELEMEN | EKSPERIMEN SEJATI | EKSPERIMEN SEMU |
| JUDUL | Pengaruh Model Pembelajaran Inkuiri Terbimbing Dengan Media Audio Visual Dan Modul Bergambar Disertai Lks Terhadap Hasil Belajar Geografi Ditinjau Dari Kemampuan Awal Dan Aktivitas Belajar Siswa (Studi Kasus Pada Materi Atmosfer) | Pengaruh Model Pembelajaran Inkuiri Terbimbing Dengan Media Audio Visual Dan Modul Bergambar Disertai Lks Terhadap Prestasi Belajar Geografi Ditinjau Dari Kemampuan Awal Dan Aktivitas Belajar Siswa (Studi Kasus Pada Materi Atmosfer) |
| MASALAH | 1. Apakah ada pengaruh antara model pembelajaran inkuiri terbimbing dengan media audio visual disertai LKS dan media modul bergambar disertai LKS Terhadap Hasil Belajar Geografi Siswa? 2. Apakah ada perbedaan hasil belajar antara siswa yang mempunyai kemampuan awal tinggi dengan siswa yang mempunyai kemampuan awal rendah ? 3. Apakah ada perbedaan hasil belajar antara siswa yang mempunyai aktivitas belajar tinggi dengan siswa yang mempunyai aktivitas belajar rendah ? | 1. Apakah ada pengaruh antara model pembelajaran inkuiri terbimbing dengan media audio visual disertai LKS dan media modul bergambar disertai LKS Terhadap Hasil Belajar Geografi Siswa? 2. Apakah ada perbedaan hasil belajar antara siswa yang mempunyai kemampuan awal tinggi dengan siswa yang mempunyai kemampuan awal rendah ? 3. Apakah ada perbedaan hasil belajar antara siswa yang mempunyai aktivitas belajar tinggi dengan siswa yang mempunyai aktivitas belajar rendah ? |
| HIPOTESIS | 1. Ada pengaruh antara model pembelajaran inkuiri terbimbing dengan media audio visual disertai LKS dan media modul bergambar disertai LKS Terhadap Hasil Belajar Geografi Siswa? 2. Ada perbedaan hasil belajar antara siswa yang mempunyai kemampuan awal tinggi dengan siswa yang mempunyai kemampuan awal rendah ? 3. Ada perbedaan hasil belajar antara siswa yang mempunyai aktivitas belajar tinggi dengan siswa yang mempunyai aktivitas belajar rendah ? | 1. Ada pengaruh antara model pembelajaran inkuiri terbimbing dengan media audio visual disertai LKS dan media modul bergambar disertai LKS Terhadap Hasil Belajar Geografi Siswa? 2. Ada perbedaan hasil belajar antara siswa yang mempunyai kemampuan awal tinggi dengan siswa yang mempunyai kemampuan awal rendah ? 3. Ada perbedaan hasil belajar antara siswa yang mempunyai aktivitas belajar tinggi dengan siswa yang mempunyai aktivitas belajar rendah ? |
| VARIABLE | a. Variabel bebas Model pembelajaran inkuiri terbimbing b. Variabel terikat Hasil belajar | a. Variabel bebas Model pembelajaran inkuiri terbimbing b. Variabel terikat Hasil belajar |
| DESAIN EKSPERIMEN | Penelitian ini menggunakan metode eksperimen sejati, dalam desain ini para subjek ditempatkan pada kelompok eksperimen dan kelompok control, melalui metode acak dan diberi tes pada variable terikat sebelum perlakuan diberikan. | Penelitian ini menggunakan metode quasi eksperimen (eksperimen semu). Dalam metode ini subjek kelompok tidak dilakukan pengacakan( berdasarkan kelas yang sudah ada) |
| TEKNIK ANALISIS | Perbedaan rata-rata skor antara pasca tes dengan pra tes untuk setiap kelompok dibandingkan untuk menentukan apakah perlakuan eksperimen menghasilkan perubahan lebih besar daripada situasi control. Pengujiannya menggunakan uji t, uji f, atau analisis kovarian | Perbedaan rata-rata skor antara pasca tes dengan pra tes untuk setiap kelompok dibandingkan untuk menentukan apakah perlakuan eksperimen menghasilkan perubahan lebih besar daripada situasi control. Pengujiannya menggunakan uji t, uji f, atau analisis kovarian |
Membangun Generasi Emas Bangsa Indonesia 2025
F TEST
Ini membandingkan penyebaran dua set data dengan membandingkan varians tersebut. Ingat bahwa Varians adalah ukuran tentang bagaimana nilai-nilai yang tersebar. Kadang-kadang juga dikenal sebagai uji Fisher. F-Test Two-sampel untuk alat analisis Varian melakukan F dua-sample-test untuk membandingkan dua varians populasi. F-test juga dikenal sebagai rasio Varians. Tes ini melibatkan menghitung varians untuk dua set data, menempatkan nilai yang lebih besar atas nilai yang lebih kecil dan kemudian melihat rasio dalam sebuah tabel.
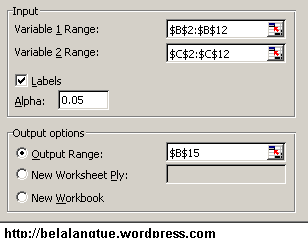
| Menggunakan F-Test Two Sample for Variances / Using F-Test Two Sample for Variances |
F-Test digunakan untuk membandingkan dua varians sampel. Asumsi bahwa mean terbesar ditempatkan pada kolom atau baris pertama.
Variable 1 Range – Masukkan data untuk kolom atau baris pertama dari data yang ingin Anda analisis.
Variable 2 Range – Masukkan data untuk kolom kedua atau baris data yang ingin Anda analisis.
Labels – Pilih jika baris atau kolom pertama dari input Anda berisi berbagai label. Hapus centang pada kotak ini jika input range Anda tidak memiliki label; Microsoft Excel label yang sesuai menghasilkan data untuk tabel output.
Alpha – Masukkan tingkat kepercayaan untuk uji ini. Nilai ini harus berada dalam jangkauan 0 … 1. Tingkat alpha tingkat signifikansi yang terkait dengan kemungkinan memiliki tipe yang Error (menolak hipotesis benar).
Output Range - Masukkan acuan bagi sel-kiri atas dari tabel output. Excel secara otomatis menentukan ukuran daerah output dan menampilkan pesan jika tabel output akan menggantikan data yang ada.
New Worksheet Ply- Klik untuk menyisipkan worksheet baru dalam workbook saat ini dan paste hasil, dimulai pada sel A1 dari lembar kerja baru. Untuk nama worksheet yang baru, ketik nama di dalam kotak.
New Workbook- Klik untuk membuat workbook baru dan paste hasil pada lembar kerja baru dalam workbook baru.
Mean – Rerata masing-masing sampel.
Variance – Varians dari masing-masing sampel.
Observations- Jumlah nilai-nilai di masing-masing sampel.
df - Derajat Kebebasan untuk masing-masing sampel.
F - F Statistik. Sebuah statistik F mendekati 1 memberikan bukti bahwa varians sampel adalah sama. Semakin tinggi statistik F semakin kecil kemungkinan bahwa hipotesis nol benar.
P(F<=f) one tail – Probabilitas bahwa
F Critical one-tail – Nilai kritis diambil dari distribusi F 0,05.
t-test
Uji-t (t-test) merupakan statistik uji yang sering kali ditemui dalam masalah-masalah praktis statistika. Uji-t termasuk dalam golongan statistika parametrik. Statistik uji ini digunakan dalam pengujian hipotesis. Seperti yang telah dibahas dalam tulisan (post) lain di weblog ini, uji-t digunakan ketika informasi mengenai nilai variance (ragam) populasi tidak diketahui. Uji-t dapat dibagi menjadi 2, yaitu uji-t yang digunakan untuk pengujian hipotesis 1-sampel dan uji-t yang digunakan untuk pengujian hipotesis 2-sampel. Bila dihubungkan dengan kebebasan (independency) sampel yang digunakan (khusus bagi uji-t dengan 2-sampel), maka uji-t dibagi lagi menjadi 2, yaitu uji-t untuk sampel bebas (independent) dan uji-t untuk sampel berpasangan (paired). Dalam lingkup uji-t untuk pengujian hipotesis 2-sampel bebas, maka ada 1 hal yang perlu mendapat perhatian, yaitu apakah ragam populasi (ingat: ragam populasi, bukan ragam sampel) diasumsikan homogen (sama) atau tidak. Bila ragam populasi diasumsikan sama, maka uji-t yang digunakan adalah uji-t dengan asumsi ragam homogen, sedangkan bila ragam populasi dari 2-sampel tersebut tidak diasumsikan homogen, maka yang lebih tepat adalah menggunakan uji-t dengan asumsi ragam tidak homogen. Uji-t dengan ragam homogen dan tidak homogen memiliki rumus hitung yang berbeda. Oleh karena itulah, apabila uji-t hendak digunakan untuk melakukan pengujian hipotesis terhadap 2-sampel, maka harus dilakukan pengujian mengenai asumsi kehomogenan ragam populasi terlebih dahulu dengan menggunakan uji-F.
Bagan yang menggambarkan bagaimana menentukan uji-t yang tepat dapat didownload di sini.
(klik kanan tulisan biru, kemudian pilih ‘save link as’)
TEORI ANALISIS REGRESI LINIER
2.1 Pengertian
Untuk mengukur besarnya pengaruh variabel bebas terhadap variabel tergantung dan memprediksi variabel tergantung dengan menggunakan variabel bebas. Gujarati (2006) mendefinisikan analisis regresi sebagai kajian terhadap hubungan satu variabel yang disebut sebagai variabel yang diterangkan (the explained variabel) dengan satu atau dua variabel yang menerangkan (the explanatory). Variabel pertama disebut juga sebagai variabel tergantung dan variabel kedua disebut juga sebagai variabel bebas. Jika variabel bebas lebih dari satu, maka analisis regresi disebut regresi linear berganda. Disebut berganda karena pengaruh beberapa variabel bebas akan dikenakan kepada variabel tergantung.
2.2 Tujuan
Tujuan menggunakan analisis regresi ialah
- Membuat estimasi rata-rata dan nilai variabel tergantung dengan didasarkan pada nilai variabel bebas.
- Menguji hipotesis karakteristik dependensi
- Untuk meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas diluar jangkaun sample.
2.3 Asumsi
Penggunaan regresi linear sederhana didasarkan pada asumsi diantaranya sbb:
- Model regresi harus linier dalam parameter
- Variabel bebas tidak berkorelasi dengan disturbance term (Error) .
- Nilai disturbance term sebesar 0 atau dengan simbol sebagai berikut: (E (U / X) = 0
- Varian untuk masing-masing error term (kesalahan) konstan
- Tidak terjadi otokorelasi
- Model regresi dispesifikasi secara benar. Tidak terdapat bias spesifikasi dalam model yang digunakan dalam analisis empiris.
- Jika variabel bebas lebih dari satu, maka antara variabel bebas (explanatory) tidak ada hubungan linier yang nyata
2.4 Persyaratan Penggunaan Model Regresi
Model kelayakan regresi linear didasarkan pada hal-hal sebagai berikut:
a. Model regresi dikatakan layak jika angka signifikansi pada ANOVA sebesar <>
b. Predictor yang digunakan sebagai variabel bebas harus layak. Kelayakan ini diketahui jika angka Standard Error of Estimate <>
c. Koefesien regresi harus signifikan. Pengujian dilakukan dengan Uji T. Koefesien regresi signifikan jika T hitung > T table (nilai kritis)
d. Tidak boleh terjadi multikolinieritas, artinya tidak boleh terjadi korelasi yang sangat tinggi atau sangat rendah antar variabel bebas. Syarat ini hanya berlaku untuk regresi linier berganda dengan variabel bebas lebih dari satu.
e. Tidak terjadi otokorelasi. Terjadi otokorelasi jika angka Durbin dan Watson (DB) sebesar <> 3
f. Keselerasan model regresi dapat diterangkan dengan menggunakan nilai r2 semakin besar nilai tersebut maka model semakin baik. Jika nilai mendekati 1 maka model regresi semakin baik. Nilai r2 mempunyai karakteristik diantaranya: 1) selalu positif, 2) Nilai r2 maksimal sebesar 1. Jika Nilai r2 sebesar 1 akan mempunyai arti kesesuaian yang sempurna. Maksudnya seluruh variasi dalam variabel Y dapat diterangkan oleh model regresi. Sebaliknya jika r2sama dengan 0, maka tidak ada hubungan linier antara X dan Y.
g. Terdapat hubungan linier antara variabel bebas (X) dan variabel tergantung (Y)
h. Data harus berdistribusi normal
i. Data berskala interval atau rasio
j. Kedua variabel bersifat dependen, artinya satu variabel merupakan variabel bebas (disebut juga sebagai variabel predictor) sedang variabel lainnya variabel tergantung (disebut juga sebagai variabel response)
2.5 Linieritas
Ada dua macam linieritas dalam analisis regresi, yaitu linieritas dalam variabel dan linieritas dalam parameter. Yang pertama, linier dalam variabel merupakan nilai rata-rata kondisional variabel tergantung yang merupakan fungsi linier dari variabel (variabel) bebas. Sedang yang kedua, linier dalam parameter merupakan fungsi linier parameter dan dapat tidak linier dalam variabel.
2.6 Uji Hipotesis
Pengujian hipotesis dapat didasarkan dengan menggunakan dua hal, yaitu: tingkat signifikansi atau probabilitas (α) dan tingkat kepercayaan atau confidence interval. Didasarkan tingkat signifikansi pada umumnya orang menggunakan 0,05. Kisaran tingkat signifikansi mulai dari 0,01 sampai dengan 0,1. Yang dimaksud dengan tingkat signifikansi adalah probabilitas melakukan kesalahan tipe I, yaitu kesalahan menolak hipotesis ketika hipotesis tersebut benar. Tingkat kepercayaan pada umumnya ialah sebesar 95%, yang dimaksud dengan tingkat kepercayaan ialah tingkat dimana sebesar 95% nilai sample akan mewakili nilai populasi dimana sample berasal. Dalam melakukan uji hipotesis terdapat dua hipotesis, yaitu:
- H0 (hipotessis nol) dan H1 (hipotesis alternatif)
Contoh uji hipotesis misalnya rata-rata produktivitas pegawai sama dengan 10 (μ x= 10), maka bunyi hipotesisnya ialah:
- H0: Rata-rata produktivitas pegawai sama dengan 10
- H1: Rata-rata produktivitas pegawai tidak sama dengan 10
Hipotesis statistiknya:
- H0: μ x= 10
- H1: μ x > 10 Untuk uji satu sisi (one tailed) atau
- H1: μ x <>
- H1: μ x ≠ 10 Untuk uji dua sisi (two tailed)
Beberapa hal yang harus diperhatikan dalam uji hipotesis ialah;
- Untuk pengujian hipotesis kita menggunakan data sample.
- Dalam pengujian akan menghasilkan dua kemungkinan, yaitu pengujian signifikan secara statistik jika kita menolak H0 dan pengujian tidak signifikan secara statistik jika kita menerima H0.
- Jika kita menggunakan nilai t, maka jika nilai t yang semakin besar atau menjauhi 0, kita akan cenderung menolak H0; sebaliknya jika nila t semakin kecil atau mendekati 0 kita akan cenderung menerima H0.
2.7 Karakteristik Model yang Baik
Model dikatakan baik menurut Gujarati (2006), jika memenuhi beberapa kriteria seperti di bawah ini:
- Parsimoni: Suatu model tidak akan pernah dapat secara sempurna menangkap realitas; akibatnya kita akan melakukan sedikit abstraksi ataupun penyederhanaan dalam pembuatan model.
- Mempunyai Identifikasi Tinggi: Artinya dengan data yang ada, parameter-parameter yang diestimasi harus mempunyai nilai-nilai yang unik atau dengan kata lain, hanya akan ada satu parameter saja.
- Keselarasan (Goodness of Fit): Tujuan analisis regresi ialah menerangkan sebanyak mungkin variasi dalam variabel tergantung dengan menggunakan variabel bebas dalam model. Oleh karena itu, suatu model dikatakan baik jika eksplanasi diukur dengan menggunakan nilai adjusted r2 yang setinggi mungkin.
- Konsitensi Dalam Teori: Model sebaiknya segaris dengan teori. Pengukuran tanpa teori akan dapat menyesatkan hasilnya.
- Kekuatan Prediksi: Validitas suatu model berbanding lurus dengan kemampuan prediksi model tersebut. Oleh karena itu, pilihlah suatu model yang prediksi teoritisnya berasal dari pengalaman empiris.
2.8 Ringkasan
Analisis regresi berbeda dengan analisis korelasi. Jika analisis korelasi digunakan untuk melihat hubungan dua variable; maka analisis regresi digunakan untuk melihat pengaruh variable bebas terhadap variable tergantung serta memprediksi nilai variable tergantung dengan menggunakan variable bebas. Dalam analisis regresi variable bebas berfungsi untuk menerangkan (explanatory) sedang variable tergantung berfungsi sebagai yang diterangkan (the explained). Dalam analisis regresi data harus berskala interval atau rasio. Hubungan dua variable bersifat dependensi. Untuk menggunakan analisis regresi diperlukan beberapa persyaratan yang harus dipenuhi.
Korelasi
Korelasi adalah metode untuk mengetahui tingkat keeratan hubungan dua peubah atau lebih yang digambarkan oleh besarnya koefisien korelasi. Koefisien korelasi adalah koefisien yang menggambarkan tingkat keeratan hubungan antar dua peubah atau lebih. Besaran dari koefisien korelasi tidak menggambarkan hubungan sebab akibat antara dua peubah atau lebih, tetapi semata-mata menggambarkan keterkaitan linier antar peubah. (Mattjik & Sumertajaya, 2000) Nilai dari Koefisien korelasi berkisar antara -1 sampai dengan 1. -1 berarti terdapat hubungan negatif (berkebalikan) yang sempurna 0 berarti tidak terdapat hubungan sama sekali 1 berarti terdapat hubungan positif yang sempurna
Banyak metode statistika untuk mengukur korelasi. Salah satu yang paling sering digunakanadalah Korelasi Pearson. Ini merupakan Metode Parametrik sehingga memerlukan pengujian asumsi, yaitu: 1. Data memiliki skala pengukuran interval atau rasio (harus numerik bukan kategorik) 2. Mengikuti Distribusi Normal 3. Memiliki hubungan linier
Apabila data Anda tidak memenuhi asumsi di atas maka gunakan korelasi yang lain, yaitu: 1. Tau Kendall 2. SpearmanCross-Tabulations
Metode Tabulasi Silang (Crosstabs)
Metode Tabulasi Silang digunakan untuk melihat hubungan antara dua variabel dalam satu tabel. Variabel yang dianalisa dengan metode ini adalah variabel yang bersifat kualitatif, yaitu yang memiliki skala nominal.
Untuk menginterpretasikan hasil pengolahan data pada tabulasi silang, ada dua hal yang perlu untuk diperhatikan, yaitu :
1. Apakah tingkat asosiasi antar variabel yang diukur tersebut signifikan atau tidak .
2. Seberapa kuat tingkat asosiasi antar variabel yang diukur tersebut.
Metode Statistik Deskriptif Frekuensi
Deskripsi atau penggambaran sekumpulan data secara visual dapat dilakukan dalam dua bagian, yaitu :
• Deskripsi dalam bentuk Tulisan/Teks. Tulisan terdiri dai bagian-bagian yang penting yang menggambarkan isi data secara keseluruhan, seperti : Mean (Rata-rata), Median (Nilai Tengah), Modus (Nilai yang paling sering muncul), Standar Deviasi (bagaimana data bervariasi dalam kelompoknya), Varians Data, Nilai Minimum dan Maksimum, dan sebagainya.
• Deskripsi dalam bentuk Gambar/Grafik. Grafik sebuah data pada umumnya disajikan untuk melengkapi deskripsi berupa teks, sehingga data tampak lebih impresif dan komunikatif. Sehingga hasil perhitungan lebih mudah dipahami.
Deskriptif Frekuensi dapat digunakan untuk menampilkan dan mendeskriptifkan (menggambarkan) data yang terdiri atas satu variabel saja. Seperti akan dibuat tabel frekuensi usia responden, maka dengan outputnya, kita dapat mengetahui berapa jumlah responden usia tertentu, rata-rata usia responden, ditambah dengan berapa standar deviasi dan sebagainya. Jika lebih dari satu variabel, maka variabel-variabel tersebut akan ditampilkan secara terpisah.
DISTRIBUSI FREKUENSI
Hasil pengukuran yang kita peroleh disebut dengan data mentah. Besarnya hasil pengukuran yang kita peroleh biasanya bervariasi. Apabila kita perhatikan data mentah tersebut, sangatlah sulit bagi kita untuk menarik kesimpulan yang berarti. Untuk memperoleh gambaran yang baik mengenai data tersebut, data mentah tersebut perlu di olah terlebih dahulu.
Pada saat kita dihadapkan pada sekumpulan data yang banyak, seringkali membantu untuk mengatur dan merangkum data tersebut dengan membuat tabel yang berisi daftar nilai data yang mungkin berbeda (baik secara individu atau berdasarkan pengelompokkan) bersama dengan frekuensi yang sesuai, yang mewakili berapa kali nilai-nilai tersebut terjadi. Daftar sebaran nilai data tersebut dinamakan dengan Daftar Frekuensi atau Sebaran Frekuensi (Distribusi Frekuensi).
Dengan demikian, distribusi frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.
Pengelompokkan data ke dalam beberapa kelas dimaksudkan agar ciri-ciri penting data tersebut dapat segera terlihat. Daftar frekuensi ini akan memberikan gambaran yang khas tentang bagaimana keragaman data. Sifat keragaman data sangat penting untuk diketahui, karena dalam pengujian-pengujian statistik selanjutnya kita harus selalu memperhatikan sifat dari keragaman data. Tanpa memperhatikan sifat keragaman data, penarikan suatu kesimpulan pada umumnya tidaklah sah.
Sebagai contoh, perhatikan contoh data pada Tabel 1. Tabel tersebut adalah daftar nilai ujian Matakuliah Statistik dari 80 Mahasiswa (Sudjana, 19xx).
Tabel 1. Daftar Nilai Ujian Matakuliah Statistik
| 79 | 49 | 48 | 74 | 81 | 98 | 87 | 80 |
| 80 | 84 | 90 | 70 | 91 | 93 | 82 | 78 |
| 70 | 71 | 92 | 38 | 56 | 81 | 74 | 73 |
| 68 | 72 | 85 | 51 | 65 | 93 | 83 | 86 |
| 90 | 35 | 83 | 73 | 74 | 43 | 86 | 88 |
| 92 | 93 | 76 | 71 | 90 | 72 | 67 | 75 |
| 80 | 91 | 61 | 72 | 97 | 91 | 88 | 81 |
| 70 | 74 | 99 | 95 | 80 | 59 | 71 | 77 |
| 63 | 60 | 83 | 82 | 60 | 67 | 89 | 63 |
| 76 | 63 | 88 | 70 | 66 | 88 | 79 | 75 |
Sangatlah sulit untuk menarik suatu kesimpulan dari daftar data tersebut. Secara sepintas, kita belum bisa menentukan berapa nilai ujian terkecil atau terbesar. Demikian pula, kita belum bisa mengetahui dengan tepat, berapa nilai ujian yang paling banyak atau berapa banyak mahasiswa yang mendapatkan nilai tertentu. Dengan demikian, kita harus mengolah data tersebut terlebih dulu agar dapat memberikan gambaran atau keterangan yang lebih baik.
Bandingkan dengan tabel yang sudah disusun dalam bentuk daftar frekuensi (Tabel 2a dan Tabel 2b). Tabel 2a merupakan daftar frekuensi dari data tunggal dan Tabel 2b merupakan daftar frekuensi yang disusun dari data yang sudah di kelompokkan pada kelas yang sesuai dengan selangnya. Kita bisa memperoleh beberapa informasi atau karakteristik dari data nilai ujian mahasiswa.
Tabel 2a.
| No | Nilai Ujian | Frekuensi |
| xi | fi | |
| 1 | 35 | 1 |
| 2 | 36 | 0 |
| 3 | 37 | 0 |
| 4 | 38 | 1 |
| : | : | : |
| 16 | 70 | 4 |
| 17 | 71 | 3 |
| : | : | 1 |
| 42 | 98 | 1 |
| 43 | 99 | 1 |
| Total | 80 |
Pada Tabel 2a, kita bisa mengetahui bahwa ada 80 mahasiswa yang mengikuti ujian, nilai ujian terkecil adalah 35 dan tertinggi adalah 99. Nilai 70 merupakan nilai yang paling banyak diperoleh oleh mahasiswa, yaitu ada 4 orang, atau kita juga bisa mengatakan ada 4 mahasiswa yang memperoleh nilai 70, tidak ada satu pun mahasiswa yang mendapatkan nilai 36, atau hanya satu orang mahasiswa yang mendapatkan nilai 35.
Tabel 2b.
| Kelas ke- | Nilai Ujian | Frekuensi fi |
| 1 | 31 – 40 | 2 |
| 2 | 41 – 50 | 3 |
| 3 | 51 – 60 | 5 |
| 4 | 61 – 70 | 13 |
| 5 | 71 – 80 | 24 |
| 6 | 81 – 90 | 21 |
| 7 | 91 – 100 | 12 |
| Jumlah | 80 |
Tabel 2b merupakan daftar frekuensi dari data yang sudah dikelompokkan. Daftar ini merupakan daftar frekuensi yang sering digunakan. Kita sering kali mengelompokkan data contoh ke dalam selang-selang tertentu agar memperoleh gambaran yang lebih baik mengenai karakteristik dari data. Dari daftar tersebut, kita bisa mengetahui bahwa mahasiswa yang mengikuti ujian ada 80, selang kelas nilai yang paling banyak diperoleh oleh mahasiswa adalah sekitar 71 sampai 80, yaitu ada 24 orang, dan seterusnya. Hanya saja perlu diingat bahwa dengan cara ini kita bisa kehilangan identitas dari data aslinya. Sebagai contoh, kita bisa mengetahui bahwa ada 2 orang yang mendapatkan nilai antara 31 sampai 40. Meskipun demikian, kita tidak akan tahu dengan persis, berapa nilai sebenarnya dari 2 orang mahasiswa tersebut, apakah 31 apakah 32 atau 36 dst.
Ada beberapa istilah yang harus dipahami terlebih dahulu dalam menyusun daftar frekuensi.
Tabel 3.
| Kelas ke- | Selang Nilai Ujian | Batas Kelas | Nilai Kelas (xi) | Frekuensi (fi) |
| 1 | 31 – 40 | 30.5 – 40.5 | 35.5 | 2 |
| 2 | 41 – 50 | 40.5 – 50.5 | 45.5 | 3 |
| 3 | 51 – 60 | 50.5 – 60.5 | 55.5 | 5 |
| 4 | 61 – 70 | 60.5 – 70.5 | 65.5 | 13 |
| 5 | 71 – 80 | 70.5 – 80.5 | 75.5 | 24 |
| 6 | 81 – 90 | 80.5 – 90.5 | 85.5 | 21 |
| 7 | 91 – 100 | 90.5 – 100.5 | 95.5 | 12 |
| Jumlah | 80 |
Range : Selisih antara nilai tertinggi dan terendah. Pada contoh ujian di atas, Range = 99 – 35 = 64
Batas bawah kelas: Nilai terkecil yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 31, 41, 51, 61, …, 91)
Batas atas kelas: Nilai terbesar yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 40, 50, 60, …, 100)
Batas kelas (Class boundary): Nilai yang digunakan untuk memisahkan antar kelas, tapi tanpa adanya jarak antara batas atas kelas dengan batas bawah kelas berikutnya. Contoh: Pada kelas ke-1, batas kelas terkecilnya yaitu 30.5 dan terbesar 40.5. Pada kelas ke-2, batas kelasnya yaitu 40.5 dan 50.5. Nilai pada batas atas kelas ke-1 (40.5) sama dengan dan merupakan nilai batas bawah bagi kelas ke-2 (40.5). Batas kelas selalu dinyatakan dengan jumlah digit satu desimal lebih banyak daripada data pengamatan asalnya. Hal ini dilakukan untuk menjamin tidak ada nilai pengamatan yang jatuh tepat pada batas kelasnya, sehingga menghindarkan keraguan pada kelas mana data tersebut harus ditempatkan. Contoh: bila batas kelas di buat seperti ini:
Kelas ke-1 : 30 – 40
Kelas ke-2 : 40 – 50:
dst.
Apabila ada nilai ujian dengan angka 40, apakah harus ditempatkan pada kelas-1 ataukah kelas ke-2?
Panjang/lebar kelas (selang kelas): Selisih antara dua nilai batas bawah kelas yang berurutan atau selisih antara dua nilai batas atas kelas yang berurutan atau selisih antara nilai terbesar dan terkecil batas kelas bagi kelas yang bersangkutan. Biasanya lebar kelas tersebut memiliki lebar yang sama. Contoh:
lebar kelas = 41 – 31 = 10 (selisih antara 2 batas bawah kelas yang berurutan) atau
lebar kelas = 50 – 40 = 10 (selisih antara 2 batas atas kelas yang berurutan) atau
lebar kelas = 40.5 – 30.5 = 10. (selisih antara nilai terbesar dan terkecil batas kelas pada kelas ke-1)
Nilai tengah kelas: Nilai kelas merupakan nilai tengah dari kelas yang bersangkutan yang diperoleh dengan formula berikut: ½ (batas atas kelas+batas bawah kelas). Nilai ini yang dijadikan pewakil dari selang kelas tertentu untuk perhitungan analisis statistik selanjutnya. Contoh: Nilai kelas ke-1 adalah ½(31+40) = 35.5
Banyak kelas: Sudah jelas! Pada tabel ada 7 kelas.
Frekuensi kelas: Banyaknya kejadian (nilai) yang muncul pada selang kelas tertentu. Contoh, pada kelas ke-1, frekuensinya = 2. Nilai frekuensi = 2 karena pada selang antara 30.5 – 40.5, hanya ada 2 angka yang muncul, yaitu nilai ujian 31 dan 38.
Teknik pembuatan Tabel Distribusi Frekuensi (TDF)
Distribusi frekuensi dibuat dengan alasan berikut:
- kumpulan data yang besar dapat diringkas
- kita dapat memperoleh beberapa gambaran mengenai karakteristik data, dan
- merupakan dasar dalam pembuatan grafik penting (seperti histogram).
Banyak software (teknologi komputasi ) yang bisa digunakan untuk membuat tabel distribusi frekuensi secara otomatis. Meskipun demikian, di sini tetap akan diuraikan mengenai prosedur dasar dalam membuat tabel distribusi frekuensi.
Langkah-langkah dalam menyusun tabel distribusi frekuensi:
- Urutkan data, biasanya diurutkan dari nilai yang paling kecil
- Tujuannya agar range data diketahui dan mempermudah penghitungan frekuensi tiap kelas!
-
- Tentukan range (rentang atau jangkauan)
- Range = nilai maksimum – nilai minimum
-
- Tentukan banyak kelas yang diinginkan. Jangan terlalu banyak/sedikit, berkisar antara 5 dan 20, tergantung dari banyak dan sebaran datanya.
- Aturan Sturges:
- Banyak kelas = 1 + 3.3 log n, dimana n = banyaknya data
-
- Tentukan panjang/lebar kelas interval (p)
- Panjang kelas (p) = [rentang]/[banyak kelas]
-
- Tentukan nilai ujung bawah kelas interval pertama
Pada saat menyusun TDF, pastikan bahwa kelas tidak tumpang tindih sehingga setiap nilai-nilai pengamatan harus masuk tepat ke dalam satu kelas. Pastikan juga bahwa tidak akan ada data pengamatan yang tertinggal (tidak dapat dimasukkan ke dalam kelas tertentu). Cobalah untuk menggunakan lebar yang sama untuk semua kelas, meskipun kadang-kadang tidak mungkin untuk menghindari interval terbuka, seperti ” ≥ 91 ” (91 atau lebih). Mungkin juga ada kelas tertentu dengan frekuensi nol.
Contoh:
Kita gunakan prosedur di atas untuk menyusun tabel distribusi frekuensi nilai ujian mahasiswa (Tabel 1).
Berikut adalah nilai ujian yang sudah diurutkan:
35 38 43 48 49 51 56 59 60 60
61 63 63 63 65 66 67 67 68 70
70 70 70 71 71 71 72 72 72 73
73 74 74 74 74 75 75 76 76 77
78 79 79 80 80 80 80 81 81 81
82 82 83 83 83 84 85 86 86 87
88 88 88 88 89 90 90 90 91 91
91 92 92 93 93 93 95 97 98 99
2. Range:
[nilai tertinggi – nilai terendah] = 99 – 35 = 64
3. Banyak Kelas:
Tentukan banyak kelas yang diinginkan.
Apabila kita lihat nilai Range = 64, mungkin banyak kelas
sekitar 6 atau 7.
Sebagai latihan, kita gunakan aturan Sturges.
banyak kelas = 1 + 3.3 x log(n)
= 1 + 3.3 x log(80)
= 7.28 ≈ 7
4. Panjang Kelas:
Panjang Kelas = [range]/[banyak kelas]
= 64/7
= 9.14 ≈ 10
(untuk memudahkan dalam penyusunan TDF)
5. Tentukan nilai batas bawah kelas pada kelas pertama.
Nilai ujian terkecil = 35
Penentuan nilai batas bawah kelas bebas saja,
asalkan nilai terkecil masih masuk ke dalam kelas tersebut.
Misalkan: apabila nilai batas bawah yang kita pilih adalah 26,
maka interval kelas pertama: 26 – 35, nilai 35 tepat jatuh
di batas atas kelas ke-1. Namun apabila kita pilih
nilai batas bawah kelas 20 atau 25, jelas nilai terkecil, 35,
tidak akan masuk ke dalam kelas tersebut.
Namun untuk kemudahan dalam penyusunan dan pembacaan TDF,
tentunya juga untuk keindahan, he2.. lebih baik kita memilih
batas bawah 30 atau 31. Ok, saya tertarik dengan angka 31,
sehingga batas bawahnya adalah 31.
Dari prosedur di atas, kita dapat info sebagai berikut:
Banyak kelas : 7
Panjang kelas : 10
Batas bawah kelas : 31
Selanjutnya kita susun TDF:
Form TDF:
------------------------------------------------------------
Kelas ke- | Nilai Ujian | Batas Kelas | Turus | Frekuensi
------------------------------------------------------------
1 31 -
2 41 -
3 51 -
: : -
6 81 -
7 91 -
------------------------------------------------------------
Jumlah
------------------------------------------------------------
Tabel berikut merupakan tabel yang sudah dilengkapi | Kelas ke- | Nilai Ujian | Batas Kelas | Frekuensi (fi) |
| 1 | 31 – 40 | 30.5 – 40.5 | 2 |
| 2 | 41 – 50 | 40.5 – 50.5 | 3 |
| 3 | 51 – 60 | 50.5 – 60.5 | 5 |
| 4 | 61 – 70 | 60.5 – 70.5 | 13 |
| 5 | 71 – 80 | 70.5 – 80.5 | 24 |
| 6 | 81 – 90 | 80.5 – 90.5 | 21 |
| 7 | 91 – 100 | 90.5 – 100.5 | 12 |
| Jumlah | 80 |
atau dalam bentuk yang lebih ringkas:
| Kelas ke- | Nilai Ujian | Frekuensi (fi) |
| 1 | 31 – 40 | 2 |
| 2 | 41 – 50 | 3 |
| 3 | 51 – 60 | 5 |
| 4 | 61 – 70 | 13 |
| 5 | 71 – 80 | 24 |
| 6 | 81 – 90 | 21 |
| 7 | 91 – 100 | 12 |
| Jumlah | 80 |
Distribusi Frekuensi Relatif dan Kumulatif
Variasi penting dari distribusi frekuensi dasar adalah dengan menggunakan nilai frekuensi relatifnya, yang disusun dengan membagi frekuensi setiap kelas dengan total dari semua frekuensi (banyaknya data). Sebuah distribusi frekuensi relatif mencakup batas-batas kelas yang sama seperti TDF, tetapi frekuensi yang digunakan bukan frekuensi aktual melainkan frekuensi relatif. Frekuensi relatif kadang-kadang dinyatakan sebagai persen.
Frekuensi relatif =
Contoh: frekuensi relatif kelas ke-1:
fi = 2; n = 80
Frekuensi relatif = 2/80 x 100% = 2.5%
| Kelas ke- | Nilai Ujian | Frekuensi relatif (%) |
| 1 | 31 – 40 | 2.50 |
| 2 | 41 – 50 | 3.75 |
| 3 | 51 – 60 | 6.25 |
| 4 | 61 – 70 | 16.25 |
| 5 | 71 – 80 | 30.00 |
| 6 | 81 – 90 | 26.25 |
| 7 | 91 – 100 | 15.00 |
| Jumlah | 100.00 |
Distribusi Frekuensi kumulatif
Variasi lain dari distribusi frekuensi standar adalah frekuensi kumulatif. Frekuensi kumulatif untuk suatu kelas adalah nilai frekuensi untuk kelas tersebut ditambah dengan jumlah frekuensi semua kelas sebelumnya.
Perhatikan bahwa kolom frekuensi selain label headernya diganti dengan frekuensi kumulatif kurang dari, batas-batas kelas diganti dengan “kurang dari” ekspresi yang menggambarkan kisaran nilai-nilai baru.
| Nilai Ujian | Frekuensi kumulatif kurang dari |
| kurang dari 30.5 | 0 |
| kurang dari 40.5 | 2 |
| kurang dari 50.5 | 5 |
| kurang dari 60.5 | 10 |
| kurang dari 70.5 | 23 |
| kurang dari 80.5 | 47 |
| kurang dari 90.5 | 68 |
| kurang dari 100.5 | 80 |
atau kadang disusun dalam bentuk seperti ini:
| Nilai Ujian | Frekuensi kumulatif kurang dari |
| kurang dari 41 | 2 |
| kurang dari 51 | 5 |
| kurang dari 61 | 10 |
| kurang dari 71 | 23 |
| kurang dari 81 | 47 |
| kurang dari 91 | 68 |
| kurang dari 101 | 80 |
Variasi lain adalah Frekuensi kumulatif lebih dari. Prinsipnya hampir sama dengan prosedur di atas.
Histogram
Histogram adalah merupakan bagian dari grafik batang di mana skala horisontal mewakili nilai-nilai data kelas dan skala vertikal mewakili nilai frekuensinya. Tinggi batang sesuai dengan nilai frekuensinya, dan batang satu dengan lainnya saling berdempetan, tidak ada jarak/ gap diantara batang. Kita dapat membuat histogram setelah tabel distribusi frekuensi data pengamatan dibuat.

Poligon Frekuensi:
Poligon Frekuensi menggunakan segmen garis yang terhubung ke titik yang terletak tepat di atas nilai-nilai titik tengah kelas. Ketinggian dari titik-titik sesuai dengan frekuensi kelas, dan segmen garis diperluas ke kanan dan kiri sehingga grafik dimulai dan berakhir pada sumbu horisontal.

Ogive
Ogive adalah grafik garis yang menggambarkan frekuensi kumulatif, seperti daftar distribusi frekuensi kumulatif. Perhatikan bahwa batas-batas kelas dihubungkan oleh segmen garis yang dimulai dari batas bawah kelas pertama dan berakhir pada batas atas dari kelas terakhir. Ogive berguna untuk menentukan jumlah nilai di bawah nilai tertentu. Sebagai contoh, pada gambar berikut menunjukkan bahwa 68 mahasiswa mendapatkan nilai kurang dari 90.5.

TABULASI DATA
Sebelum melakukan analisa data, dilakukan terlebih dahulu tahapan pra analisa data berupa penyuntingan, verifikasi, dan tabulasi data. Pasca pengumpulan data di lapangan merupakan proses memasuki tahapan pra analisa. Tabulasi data biasanya memang tidak dimasukkan dalam prosedur analisa data riset, karena belum mengungkapkan hubungan data hasil riset. Namun sedikitnya tabulasi data ini dapat menyajikan pra analisa berupa ukuran deskriptif masing-masing variabel pengamatan. Tahapan awal pra analisa, data hasil survey yang telah dicek oleh supervisor lapangan di-entry pada program komputer. Dahulu sebelum program komputer berkembang, data hasil survey dikumpulkan dan dianalisa secara manual. Tentunya ini akan merepotkan untuk survey yang melibatkan banyak responden.
Proses entry atau pengetikan/pemasukan data secara sederhana dapat menggunakan program MS Excel atau langsung pada program aplikasi statistik seperti SPSS, Minitab, STATA, atau Lisrel. Namun khusus program aplikasi statistik tersebut, data harus dikodifikasi (data coding) secara numerik terlebih dahulu agar dapat dianalisa. Gambar berikut menampilkan tahapan yang perlu dilakukan proses pra analisa:
Hal penting yang perlu diperhatikan, yakni terjadinya kesalahan saat pengetikan atau mengkodifikasi jawaban yang berdampak pada kesalahan fatal pada analisa data. Seperti dalam skala likert: “1 - 5” = “sangat tidak puas – sangat puas”, jangan terbalik mengkodifikasikan “sangat tidak puas” = “5”. Beberapa perusahaan riset pemasaran atau lembaga survey umumnya menggunakan program khusus data entry, coding, dan tabulation dalam satu kesatuan. Sehingga mempermudah proses pra analisa sekaligus meminimalisasi terjadinya kesalahan pengetikan dan memasukkan data. Program khusus tersebut seperti Quantum, QPS, atau CS-Pro dapat di-setting tampilan layarnya nampak seperti kuesioner asli. Apabila program tersebut sudah di-setting sebelumnya, peng-entry-an data dapat dilakukan terpisah oleh siapapun meski bukan periset semula.
Pengontrolan data setelah supervisor lapangan adalah Data Entry Officers, yakni penyuntingan dan pengecekan apabila terdapat satu dua jawaban kuesioner yang tidak terisi, tidak lengkap, atau tidak terbaca. Apabila hal itu terjadi, dapat dilakukan konfirmasi secepatnya kepada interviewer bersangkutan melalui supervisor lapangan. Namun pengontrolan ini hanya ditoleransikan bagi kesalahan kecil tanpa perlu konfirmasi ulang terhadap responden yang terkait. Sementara untuk kesalahan besar dapat dilakukan penolakan (“reject”) atas kuesioner yang telah dikumpulkan.
Adakalanya terjadi satu-dua jawaban kuesioner kosong tidak terisi dan periset sendiri kesulitan untuk mengkonfirmasi ulang responden, interviewer, atau supervisor bersangkutan. Kebijakan penolakan dapat ditoleransi apabila kurang dari 5 % dari seluruh sampel responden. Kekosongan atau kehilangan nilai data ini dapat disiasati pada program SPSS dengan replace missing value (RMV). Dengan RMV, data yang hilang tadi akan diganti dengan pendekatan statistik, seperti pendekatan rata-rata, median, interpolasi linier, atau interpolasi trend. Barulah, setelah penyuntingan dan pengecekkan data dilakukan sesuai ambang toleransi kesalahan dan acuan jumlah sampel bersih. Data mentah yang telah disunting dan dicek disebut raw data yang adakalanya klien atau pihak pengguna memintanya sebagai bukti lapangan dan lampiran laporan akhir riset.
Aplikasi Statistika dalam Penelitian Kuantitatif
Distribusi Frekuensi
Teknik ini mungkin merupakan teknik yang paling mudah dan paling banyak digunakan untuk mendeskripsikan data. Distribusi frekuensi mengindikasikan jumlah dan persentase responden, obyek yang masuk ke dalam kategori yang ada.
Teknik ini biasanya digunakan untuk memberikan informasi awal dalam penelitian tentang obyek atau responden.
Cross-Tabulations
Bila distribusi frekuensi digunakan untuk memberikan informasi yang menggambarkan keseluruhan sampel atau populasi yang diteliti, cross-tabulation adalah sebuah teknik visual yang memungkinkan peneliti menguji relasi antar variabel.
Kedua teknik yang telah disebutkan di atas digunakan untuk menggambarkan data yang dikumpulkan selama penelitian, ini hanya merupakan awal tugas peneliti. Tugas berikutnya adalah menjelaskan temuan-temuan ini dan dapat membuat sebuah generalisasi tentang populasi yang lebih besar. Maka digunakanlah inferential statistics.
Korelasi
Metode ini menggambarkan secara kuantitatif asosiasi ataupun relasi satu variabel interval dengan variabel interval lainnya. Sebagai contoh kita dapat lihat relasi hipotetikal antara lamanya waktu belajar dengan nilai ujian tinggi.
Korelasi diukur dengan suatu koefisien (r) yang mengindikasikan seberapa banyak relasi antar dua variabel. Daerah nilai yang mungkin adalah +1.00 sampai -1.00. Dengan +1.00 menyatakan hubungan yang sangat erat, sedangkan -1.00 menyatakan hubungan negatif yang erat.
Berikut ini adalah panduan untuk nilai korelasi tersebut :
+ atau - 0.80 hingga 1.00 korelasi sangat tinggi
0.60 hingga 0.79 korelasi tinggi
0.40 hingga 0.59 korelasi moderat
0.20 hingga 0.39 korelasi rendah
0.01 hingga 0.19 korelasi sangat rendah
Satu hal yang perlu diingat adalah "korelasi tidak menyatakan hubungan sebab-akibat". Dari contoh di atas, korelasi hanya menyatakan bahwa ada relasi antara lamanya waktu belajar dengan nilai ujian tinggi, namun bukan "lamanya waktu belajar menyebabkan nilai ujian tinggi".
Regresi
Regresi digunakan ketika periset ingin memprediksi hasil atas variabel-variabel tertentu dengan menggunakan variabel lain. Dalam bentuknya yang paling sederhana yang hanya melibatkan dua buah variabel, yaitu variabel bebas (independent) dan variabel terikat (dependent), misalnya lama waktu belajar dengan nilai ujian. Regresi sederhana berusaha memprakirakan nilai ujian dengan lamanya waktu belajar.
Analisis regresi mengindikasikan kepentingan relatif satu atau lebih variabel dalam memprediksi variabel lainnya.
t-test
Teknik t-test digunakan bila periset ingin mengevaluasi perbedaan antara efek. Sebagai contoh, periset mungkin tertarik dalam perbedaan kepuasan kerja untuk orang-orang yang berbeda tingkat pendidikannya. Teknik analisis yang banyak digunakan adalah membandingkan dua kelompok, misalnya mereka yang mendapat pendidikan universitas dengan mereka yang tidak, dengan menggunakan mean kelompok sebagai dasar perbandingan. t-test akan mengindikasikan apakah perbedaan antara kedua kelompok tersebut signifikan secara statistika.
F-test
F-test menguji apakah populasi tempat sampel diambil memiliki korelasi multiple (R) nol atau apakah terdapat sebuah relasi yang signifikan antara variabel-variabel independen dengan variabel-variabel dependen.
Analisis Validitas
Untuk melakukan analisis validitas dapat digunakan metode Pearson Product Moment (bila sampel normal, 30) ataupun metode Spearman Rank Correlation (bila sampel kecil, 30).
Analisis Reliabilitas Internal
Untuk analisis reliabilitas internal dapat digunakan metode Cronbach's Alpha. Jika koefisien yang didapat 0.60, maka instrumen penelitian tersebut reliabel.
Tipe Data
Setiap data memiliki tipe data, apakah merupakan angka bulat ( integer ), angka biasa ( real ), atau berupa karakter ( char ), dan sebagainya.
Ada 2 kategori dari tipe data yaitu:
1. Tipe dasar
- Bilangan atau angka yang tidak memiliki titik desimal atau pecahan, seperti 10, +225, -10,+25.
- Tipe dituliskan sebagai integer atau int
- Jangkauan nilai bergantung pada implementasi perangkat keras komputer, misalnya dari -11 s/d +12; untuk algoritma tidak kita batasi.
- Operasi aritmetik: tamabah+, kurang-, kali*, bagi/, sisa hasil bagi%
- Operasi pembanding:lebih kecil=, sama=, tidak sama>< .
- Bilangan atau angka yang bisa memiliki titik desimal atau pecahan, dan ditulis sebagai : 235.45, +13.99, -87.76 atau dalam notasi ilmiah seperti : 1.245E+03, 7.45E-02, dsb.
- Tipe dituliskan sebagai : real
- Jangkauan nilai : bergantung pada implementasi perangkat keras komputer, misalnya dari -2.9E-39 s/d +1.7E+38, untuk algoritma tidak dibatasi.
- Operasi aritmatik dan pembandingan juga berlaku bagi bilangan biasa.
3. Bilangan tetap ( const ).
- Bilangan tetap ( const ) adalah tipe bilangan, tidak bernilai bulat maupun tidak, yang nilainya tidak berubah selama algoritma dilaksanakana.
- Tipe dituliskan sebagai const .
- Jangkauan nilai meliputi semua bilangan yang mungkin.
4. Karakter ( character )
- Karakter adalah data tunggal yang mewakili semua huruf, simbol baca, dan juga simbol angka yang tidak dapat dioprasikan secara matematis, misalnya: ’A’, ’B’, .....,’Z’, ’?’,’!’, dst.
- Tipe dituliskan sebagai char
- Jangkauan nilai meliputi semua karakter dalam kode ASCII, atau yang tertera pada setiap tombol keyboard.
- Operasi pembanding dapat dilakukan dan dievaluasi menurut urutan kode ASCII, sehingga huruf ’A’ (Hex 41) sebenarnya lebih kecil dari huruf ’a’ (Hex 61).
5. Logik ( logikal )
- Tipe data logik adalah tipe data yang dipergunakan untuk memberi nilai pada hasil pembandingan, atau kombinasi pembandingan.
- Tipe dituliskan sebagai boolean
- Jangkauan nilai ada dua : true dan false
2. Tipe bentukan
1. Array ( larik )
- Array adalah tipe data bentukan, yang merupakan wadah untuk menampung beberapa nilai data yang sejenis. Kumpulan bilangan bulat adalah array integer, kumpulan bilangan tidak bulat adalah array real.
- Cara menefinisikan ada 2 macam, yaitu:
* Nilai_ujian : array [ 1..10] of integer, atau * Int nilai_ujian[10];
- Kedua definisi diatas menunjukkan bahwa nilai_ujian adalah kumpulan dari 10 nilai bertipe bilangan bulat.
2. String
- String adalah tipe data bentukan yang merupakan deretan karakter yang membentuk satu kata atau satu kalimat, yang biasanya diapit oleh dua tanda kutip.
- Sebagai contoh: nama, alamat, dan judul adalah tipe string.
- Cara mendefinisikannya adalah:
* string nama, alamat; atau * nama,alamat : string;
3. Record ( rekaman )
- Record adalah tipe data bentukan yang merupakan wadah untuk menampung elemen data yang tipenya tidak perlu sama dengan tujuan mewakili satu jenis objek.
- Sebagai contoh, mahasiswa sebagai satu jenis objek memiliki beberapa elemen data seperti : nomer_stb, nama, umur, dll.
- Cara mendefinisikan record mahasiswa tersebut adalah sebagai berikut:
Type dataMhs : record
nomer_stb : integer,
Nama_mhs : string,
Umur : integer,
2. Variabel
Variabel adalah nama yang mewakili suatu elemen data seperti : jenkel untuk jenis kelamin, t4lahir untuk tempat lahir, dan sebagainya. Ada aturan tertentu yang wajib diikuti dalam pemberian nama variable, antara lain:
* Harus dimulai dengan abjad, tidak boleh dengan angka atau symbol. * Tidak boleh ada spasi diantaranya * Jangan menggunakan simbol yang bisa membingungkan seperti titik dua, titik koma, koma, dan sebagainya. * Sebaiknya memiliki arti yang sesuai dengan elemen data. * Sebaiknya tidak terlalu panjang.
Contoh variabel yang benar : Nama, Alamat, Nilai_ujian
Contoh variabel yang salah : 4XYZ, IP rata, Var;=xy,45GURU DAN PBM
Tips Bagi Ayah dan Ibu Yang Bekerja
Membesarkan anak dengan baik memang tidak mudah bagi pasangan suami-istri yang bekerja. Dengan panduan berikut mudah-mudahan Anda dapat me...

Mengenai Saya

- KURNIA TRIYULI
- It is not how much we have, but how much we enjoy, that makes happiness
Translate
Total Tayangan Halaman
Labels
- alam (69)
- aleut (1)
- ANTROPOSFER (1)
- bahan ajar (11)
- BATIK MALANGAN (1)
- BATUAN DAN MINERAL (10)
- bentuk muka bumi (7)
- BENUA (14)
- bimbingan belajar (48)
- BIOMA (11)
- BUAH (12)
- BUDAYA INDONESIA (5)
- buku psikologi (15)
- BUNAKEN (3)
- citra penginderaan jauh (53)
- DEFINISI GEOGRAFI (3)
- demografi (35)
- EVALUASI PEMBELAJARAN (10)
- FENOMENA (30)
- flora dan fauna (28)
- GEOGRAFI EKONOMI (2)
- geografi hewan (15)
- GEOGRAFI LINGKUNGAN (25)
- GEOGRAFI PERTANIAN (23)
- geografi tumbuhan (23)
- geologi (70)
- geomorfologi (36)
- GLOBALISASI (1)
- GURU DAN PBM (34)
- HARI BUMI (2)
- HIDROLOGI (7)
- hipnotis (18)
- HUJAN ASAM (3)
- ilmu tanah (6)
- imahagi (4)
- informasi (57)
- INTERPRETASI CITRA (54)
- IPS SD (28)
- JUDUL PENELITIAN (1)
- KAMUS GEOGRAFI (1)
- kartografi (12)
- keajaiban dunia (3)
- kebudayaan (2)
- KECERDASAN (25)
- KELAS IX SEM 1: EKONOMI (10)
- KELAS IX SEM 1: GEOGRAFI (6)
- KELAS IX SEM 1: SEJARAH (4)
- KELAS IX SEM 1: SOSIOLOGI (1)
- KELAS IX SEM 2: EKONOMI (4)
- KELAS IX SEM 2: GEOGRAFI (70)
- KELAS IX SEM 2: SEJARAH (11)
- KELAS IX SEM 2: SOSIOLOGI (2)
- KELAS VII SEM 1 : SOSIOLOGI (2)
- KELAS VII SEMESTER 1 (7)
- KELAS VIII SEM 1: SOSIOLOGI (1)
- KELAS VIII SEMESTER 2 EKONOMI (8)
- KELAS VIII SEMESTER 2 GEOGRAFI (4)
- KELAS VIII SEMESTER 2 SEJARAH (2)
- KELAS VIII SEMESTER 2 SOSIOLOGI (4)
- KEMAMPUAN LAHAN (2)
- KERJASAMA INTERNASIONAL (7)
- KESESUAIAN LAHAN (10)
- KLIMATOLOGI (25)
- KONSEP DASAR GEOGRAFI (1)
- KONSEP DASAR IPS (1)
- kosmografi (123)
- KRISTAL (28)
- KUE (1)
- KUIS PSIKOLOGI (8)
- KUTUB (5)
- LAUT JEPANG (7)
- lingkungan hutan tropis (5)
- lokasi wisata alam (8)
- LPJ (1)
- MASALAH SOSIAL (2)
- MATERI FLASH (12)
- MATERI GEOGRAFI KELAS VII (52)
- MATERI GEOGRAFI KELAS VIII SEMESTER 2 (41)
- materi kelas viii (34)
- materi kelas x (15)
- materi kelas xii (10)
- MEDIA PEMBELAJARAN (5)
- menu (5)
- metklim (34)
- MIGRASI HEWAN (3)
- NATIONAL GEOGRAPHIC (2)
- NEGARA (20)
- negara berkembang (29)
- negara maju (17)
- obyek wisata (7)
- OLEH-OLEH DARI ROTE (4)
- olimpiade kebumian (1)
- OSEANOGRAFI (53)
- OTAK (7)
- palaentologi (2)
- PANTAI PRIGI (1)
- pemanasan global (14)
- pembelajaran (36)
- pembelajaran alam (4)
- penduduk (26)
- pengantar geografi (8)
- pengetahuan agama (2)
- pengetahuan komputer (10)
- PENGETAHUAN UMUM (10)
- penjelajahan (7)
- perdagangan internasional (1)
- PERGERAKAN NASIONAL (11)
- PERISTIWA GEOGRAFI (2)
- PERKEMBANGAN ANAK (35)
- PETA INTERAKTIF (2)
- PROPOSAL (1)
- PTK (4)
- PULAU (1)
- RELIEF DASAR LAUT (1)
- RESEP MASAKAN (7)
- RPP DAN SILABUS KARAKTER BANGSA (4)
- RUMAH (26)
- sedimentasi (1)
- sejarah (25)
- SEJARAH INDONESIA (11)
- selingan (16)
- seni dapur (3)
- SILABUS GEOGRAFI (4)
- SINEMATOGRAFI (12)
- situs peninggalan sejarah (21)
- SOAL GEOGRAFI (2)
- sosiologi (12)
- STATISTIK (17)
- SUAKA ALAM DAN SUAKA MARGASATWA (45)
- suku bangsa (4)
- TAMAN (9)
- TAMAN NASIONAL (45)
- tanaman langka (11)
- TANAMAN OBAT TRADISIONAL (1)
- teknologi (10)
- TELAAH KURIKULUM (3)
- tenaga eksogen (11)
- tenaga endogen (6)
- TENGGER (2)
- tentang otak (11)
- THE GEOGRAPHY DEPARTEMENT (10)
- tips dan trik (74)
- TSUNAMI (1)
- tubuh kita (92)
- UKG (2)
- UNDANG-UNDANG TENTANG PENDIDIKAN (2)
Entri Populer
-
Tugas :Ahmad Syaifuddin Hasan I. Definisi Kata ”cerdas” menurut Goleman mengandung dua arti, pertama cerdas pikiran dan kedua cerdas e...
-
Model pembelajaran pelajaran Ilmu Pengetahuan Sosial (IPS) bagi murid sekolah dasar hendaknya sesuai dengan kebutuhan anak usia sekolah...
-
Sukses menjadi guru tak semata-mata karena menenteng ijazah dari fakultas keguruan atau mendapat sertifikasi profesional. Guru keren di mat...
-
Kegiatan Mengajar dan Mengelola Kelas Kegiatan guru didalam kelas meliputi dua hal pokok, yaitu mengajar dan mengelola kelas. Kegiatan m...
-
TULIP LAUT UNGU Tiga Laut Jepang Perairan di lepas pantai bervariasi mulai dari dingin, sedang, hingga tropis. Kehidupan lautnya pun sam...
-
Mendesak, rencana tata ruang berkelanjutan untuk konservasi Papua Mulai hari ini (12/11) hingga Sabtu (14/11) diselenggarakan konfer...
-
Gunung Merapi, teraktif didunia Gunung Merapi berada di Pulau Jawa pada rangkaian gunungapi aktif sebelah selatan, Gunung Merapi me...
-
Pengungsi iklim Pernah dengar istilah pengungsi iklim? Pengungsi iklim adalah populasi manusia yang akan terusir dari tempat tingga...
-
Nama : SHILVIA AYU RHOMANTIKA Kelas : Regular 2008 Pokjar : Jenu A. hakikat dan sejarah IPS Seper...
-
Plastik biologis belum tentu ramah lingkungan Plastik biologis yang terbuat dari tanaman ternyata...